This column was originally published in the Roanoke Beacon the week of July 28th, 2021.
In one of my earlier contributions I tried to show that and how rational thinking leads to irrational thinking. Here now, I would like to show the opposite. I will prove to you that 1 = 5 and then show you how this seeming nonsense can make a lot of sense.
In mathematics, we start with natural numbers: 1, 2, 3, etc. Eventually, we arrive at negative numbers, when we subtract a number that is larger than the number from which it is subtracted. As in 3 – 5 = -2. We multiply and divide, which eventually leads to exponential numbers as in 2 in the 3rd power = 2 x 2 x 2 = 23 = 8. The reversal of exponential calculation is root extraction: the third root of 8 is 2. Applying the established and proven calculating rules of mathematics, we will eventually have to draw the square root of -1 (minus one). √-1 , however, is impossible because -1 x -1 is 1 and 1 x 1 is also 1. No number multiplied with itself produces a negative product. Such a situation should really not exist. A number must have only one value and be identical only with itself or the entire foundation of mathematical thinking collapses. Two different identities for the same number would also be inconsistent with the mathematical proof of Complete Induction, which proves that whatever relationship exists between two natural numbers also applies to any other two natural numbers. In philosophy, such a situation is called an ‘aporia’. In vernacular speech it is called a dead-end. If one accepted the reasoning that it is impossible to calculate the square root of -1, all mathematics would end here. The German mathematician Gottfried Wilhelm Leibniz (1646 – 1716), a contemporary of Isaac Newton, and probably the original inventor of calculus, came up with what we would today call a “black box” idea. He simply gave the conundrum a name and stopped worrying whether it made sense or not. He called the square root of -1 “i” – for “imaginary number”, and continued to apply the established calculating methods and rules for equations, such as e.g. that an equation remains a valid equation as long as the same operation is carried out on both sides of it. We can therefore write the following equations:
i = √-1
i2 = -1 (The root is removed by raising i to the second power)
i3 = -i (Both sides of the equation are multiplied x i. Since i2 = -1 , -1 x i = -i)
i4 = 1 (Both sides of the equation are multiplied x i. 14 = i2 x i2 = -1 x -1 = 1)
i5 = i (Both sides of the equation are multiplied x i. i4 x i = 1 x i = i)
Any single number can be expressed as n1 i.e. that number in the first power. This means that i = i1. This means that if i5 = i is true, then i5 = i1 is also true. Ergo: i5 = i1 .
Since this is still an equation and since the base is “i” on both sides of the equation, and since i = i , 5 the exponents on both sides of the equation must also be equal.
Ergo:
5 = 1
q.e.d.
OK, we have proven that 5 = 1, but is there any context in which this might be true or have any meaning? Indeed, it is true in the Unit Circle, when you count the quadrants. If you do not believe me, look at your wristwatch: 1 or 5 (0 or 12 h) equals North or zero or 360 degrees; 2 (3 or 1500 h) equals East, or 90 degrees; 3 (6 or 1800 h) equals South or 180 degrees; and 4 (9 or 21 h) equals West or 270 degrees.
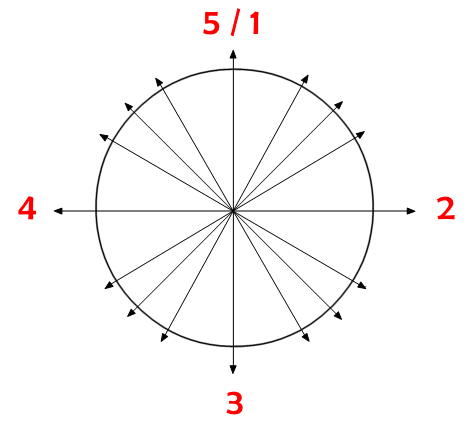
The unit circle is the basis of trigonometry.
Trigonometry is the basis of Spherical Trigonometry.

Spherical Trigonometry is the basis of understanding space and the universe.
Conclusions
We started with a seeming aporia. We decided to treat it like a black box, give it a name, and continue to apply the established rules of calculating and equations. This led us to the equation of 1 = 5. We found that this makes indeed sense in the unit circle, which is the gateway to trigonometry, which itself is the gateway to spherical trigonometry, which is the first step to understanding the universe and navigation in space. The exercise shows that the universe can be described in mathematical terms (Newton and Leibniz are nodding in agreement). It further shows that the universe has a mathematical structure of sublime intelligence and that humans (with a little effort) are capable of understanding this structure (or at least part of it). The exercise also illustrates, how the black-box method of thinking can be used to turn a seeming dead-end into a door opener and send us on a path to deeper understanding of reality at a higher level of abstraction.
I should add that we can calculate with the imaginary number i as if it were a natural number, applying the established rules of calculation and equations, and we can use it to build bridges that hold and airplanes that fly. You may apply Leibniz’ approach to other situations in life and you may find that what seems to make little sense at first, turns out to make a lot of sense – just change our approach!